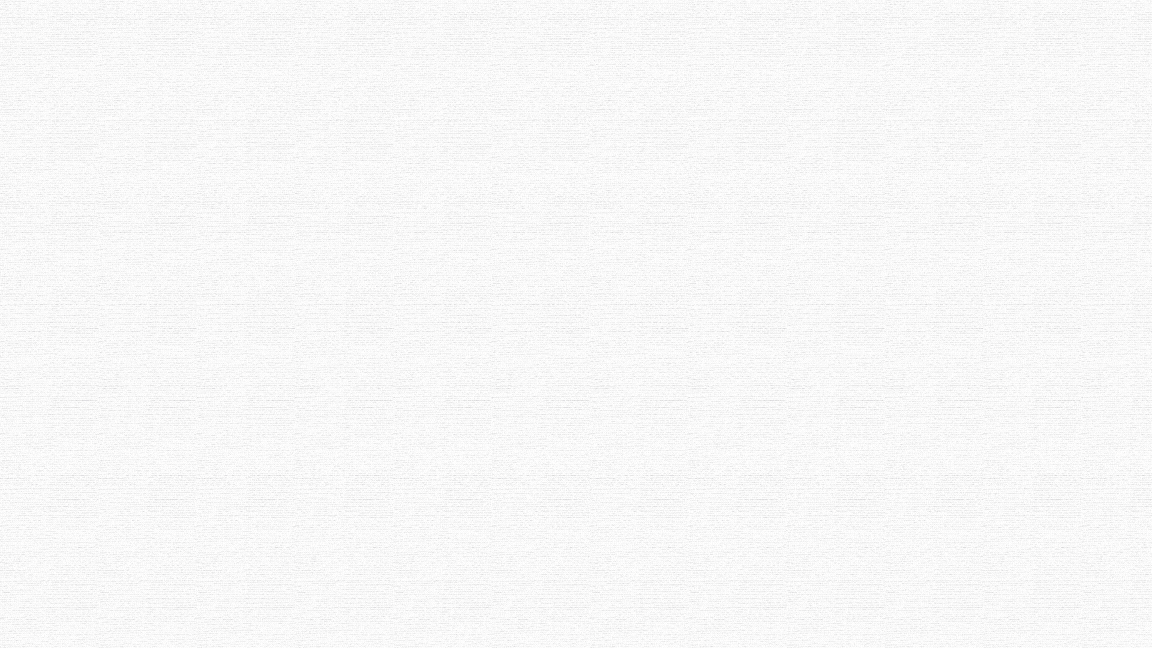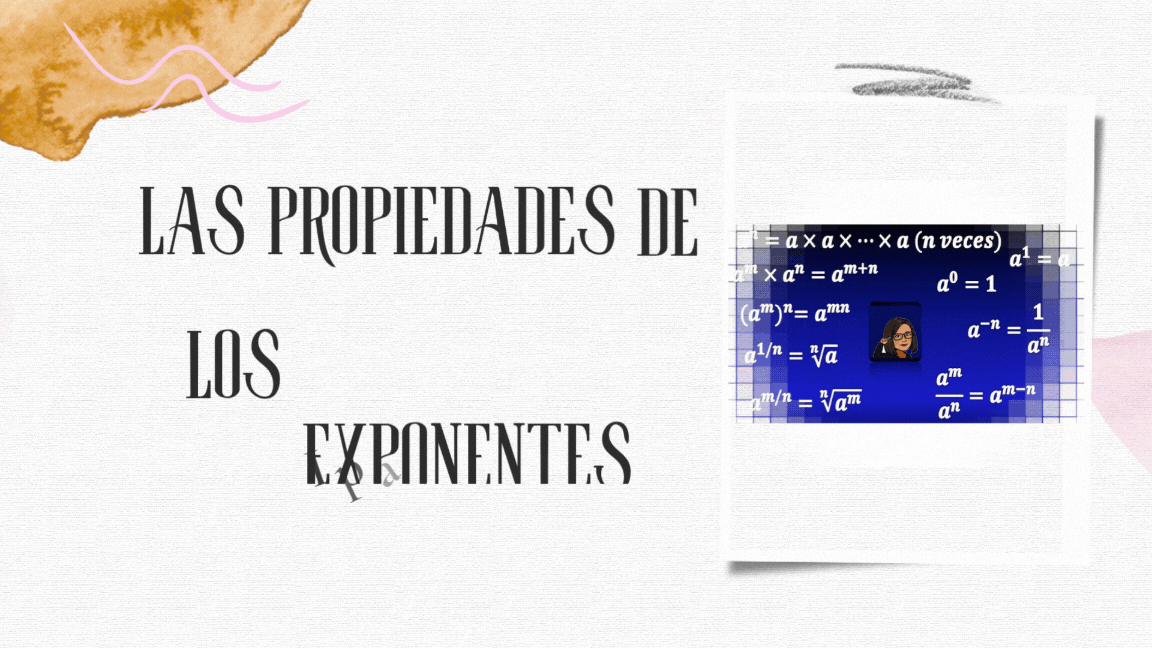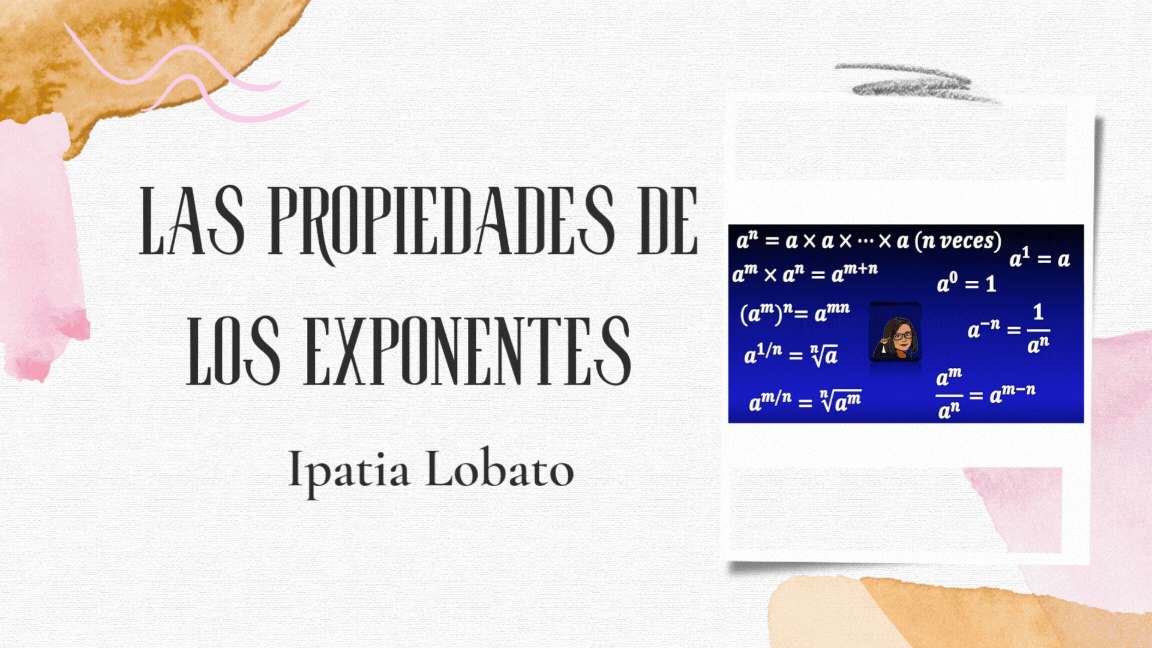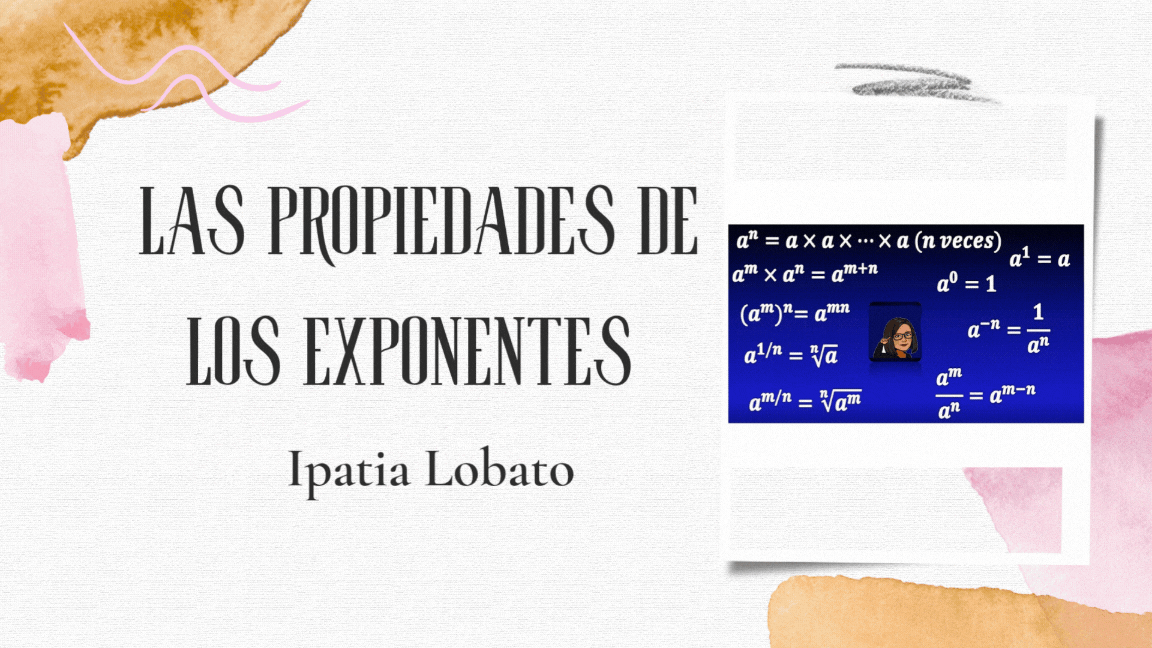• Bienvenida

    Bienvenido a Mil Aulas 

    Las propiedades de los exponentes 

     

     ¡Bienvenidos al emocionante mundo de las potencias y exponentes!  Si alguna vez te has preguntado cómo los números pueden crecer de manera tan rápida y sorprendente, ¡estás en el lugar correcto! En este blog vamos a explorar cómo los exponentes transforman los números comunes en superpoderes matemáticos. Desde lo más básico hasta trucos sorprendentes, te enseñaremos cómo las potencias son como un ataque de velocidad para las matemáticas. ¿Te atreves a descubrir cómo algo tan sencillo como un número elevado a una potencia puede hacer que las cosas se vuelvan gigantescas? ¡Vamos a despejar todas tus dudas y a convertirte en un maestro de las potencias!  ¡Sigue leyendo y que comience la aventura matemática!

    Experiencia laboral:

    Licenciada en matemáticas

    PROPIEDADES DE LOS EXPONENTES (CARACTERIZACIÓN)

    Los exponentes son una forma abreviada de expresar multiplicaciones repetidas de un mismo número o expresión. Entender las propiedades de los exponentes es fundamental para simplificar y manipular expresiones algebraicas de manera eficiente. Estas propiedades permiten operar potencias con la misma base o con diferentes bases, facilitando la resolución de problemas matemáticos que involucran potencias. En esta caracterización, se describen las reglas básicas que gobiernan el comportamiento de los exponentes, junto con ejemplos que ilustran su aplicación práctica.

    1. Producto de potencias con la misma base

    Regla:

    am⋅an=am+na^m \cdot a^n = a^{m+n}

    Caracterización:
    Cuando multiplicas potencias con la misma base, se suman los exponentes.
    Ejemplo:

    23⋅24=23+4=272^3 \cdot 2^4 = 2^{3+4} = 2^7

    2. Cociente de potencias con la misma base

    Regla:

    aman=am−n,a≠0\frac{a^m}{a^n} = a^{m-n}, \quad a \ne 0

    Caracterización:
    Cuando divides potencias con la misma base, se restan los exponentes.
    Ejemplo:

    5652=56−2=54\frac{5^6}{5^2} = 5^{6-2} = 5^4

    3. Potencia de una potencia

    Regla:

    (am)n=am⋅n(a^m)^n = a^{m \cdot n}

    Caracterización:
    Cuando tienes una potencia elevada a otra potencia, multiplicas los exponentes.
    Ejemplo:

    (32)4=32⋅4=38(3^2)^4 = 3^{2\cdot4} = 3^8

    4. Potencia de un producto

    Regla:

    (ab)n=an⋅bn(ab)^n = a^n \cdot b^n

    Caracterización:
    Cuando una multiplicación está elevada a un exponente, cada factor se eleva al exponente.
    Ejemplo:

    (2⋅5)3=23⋅53=8⋅125=1000(2 \cdot 5)^3 = 2^3 \cdot 5^3 = 8 \cdot 125 = 1000

    5. Potencia de un cociente

    Regla:

    (ab)n=anbn,b≠0\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}, \quad b \ne 0

    Caracterización:
    Al elevar una fracción a un exponente, se eleva tanto el numerador como el denominador.
    Ejemplo:

    (23)2=2232=49\left(\frac{2}{3}\right)^2 = \frac{2^2}{3^2} = \frac{4}{9}

    6. Exponente cero

    Regla:

    a0=1,a≠0a^0 = 1, \quad a \ne 0

    Caracterización:
    Cualquier número distinto de cero elevado a la potencia cero es igual a 1.
    Ejemplo:

    70=17^0 = 1

    7. Exponente negativo

    Regla:

    a−n=1an,a≠0a^{-n} = \frac{1}{a^n}, \quad a \ne 0

    Caracterización:
    Un exponente negativo convierte la potencia en su recíproco.
    Ejemplo:

    2−3=123=182^{-3} = \frac{1}{2^3} = \frac{1}{8}

    UCE

                           
    (Puede editar o eliminar este texto)

Cursos disponibles

Las propiedades de los exponentes

Las propiedades de los exponentes constituyen un pilar fundamental en el estudio del álgebra, ya que permiten simplificar y manipular expresiones matemáticas que involucran potencias de manera sistemática y coherente. Estas reglas facilitan operaciones como la multiplicación, división y potenciación de potencias, además de dar sentido a exponentes cero y negativos, que amplían la definición de potencia más allá de la multiplicación repetida.

Comprender estas propiedades no solo desarrolla habilidades algebraicas esenciales, sino que también fortalece el razonamiento matemático, ya que se basa en patrones lógicos y la generalización de procesos. En la enseñanza, es crucial que los estudiantes internalicen estas reglas para abordar con confianza problemas más complejos en álgebra, cálculo y otras ramas de las matemáticas.